Теория электрической связи
1. Общие сведения о системах связи
1.1. Информация, сообщения, сигналы
Под информацией понимают совокупность каких-либо сведений о явлениях, объектах и т.п. Сообщения представляют собой материальную форму существования информации и могут иметь различную физическую природу. Сигналами в электрической связи служат процессы (функции времени) электрической природы, посредством которых осуществляется передача сообщений на расстояние. Общее и различное в этих основополагающих понятиях теории связи поясняется таблицей 1.1. В ней также указаны возможные преобразователи сообщений в сигналы, которые называют датчиками сигналов.
Таблица 1.1.
| Вид
сообщения |
Математ.
модель |
Сигнал
u(t) |
Датчик
сигнала |
 |
ai (k)
k = 1,2,…,n ai Î {aj}, j = 1,2,….m |
u(t)
t m = 2, n = 6 |
Клавиатура
ЭВМ |
 |
p = p(t) | u(t)
t
|
Микрофон |
 Видео |
b = b(x,y)
b = b(x,y,t) |
u(t)
t
|
ФЭ и УР
Видеокамера |
Текстовые сообщения представляют собой последовательности символов из некоторого конечного множества {ai} (языка) с известным объемом алфавита m. Преобразование такого рода сообщений в сигнал может осуществляться, например, клавиатурой ЭВМ путем поочередного кодирования отдельных символов сообщения k-разрядными комбинациями из 0 и 1, которым соответствуют два разных уровня напряжения.
Звуковые сообщения представляют собой изменения давления воздушной среды в заданной точке пространства во времени p(t). С помощью микрофона они преобразуются в переменный электрический сигнал u(t), который в определенном смысле является копией сообщения и отличается от него лишь физической размерностью.
Видеосообщения
можно рассматривать как распределение яркости на поверхности объекта b(x,y), неподвижное изображение которого требуется передать на расстояние (фототелеграф), или более сложный процесс b(x,y,t) (черно-белое телевидение).
Характерной особенностью при передаче видеосообщений является необходимость преобразования описывающих их многомерных функций в одномерный сигнал u(t). Это достигается использованием в датчиках видеосигналов устройств развертки (УР) для поэлементного преобразования яркости отдельных точек объектов в уровень электрического сигнала с помощью фотоэлементов (ФЭ) или иных фотоэлектрических преобразователей.
Классификация сигналов
По относительной ширине спектра сигналы делят на низкочастотные (называемые также НЧ, видео, широкополосные сигналы) и высокочастотные (ВЧ, радио, узкополосные, полосовые сигналы).
Для НЧ сигналов ?F/Fср
> 1, где
?F
= Fmax – Fmin – абсолютная ширина спектра сигнала,
Fср
= (Fmax + Fmin)/2 – средняя частота спектра сигнала,
Fmax – максимальная частота в спектре сигнала,
Fmin – минимальная частота в спектре сигнала.
Для ВЧ сигналов ?F/Fср << 1.
Как правило, первичные сигналы на выходе датчиков являются низкочастотными. Полезно помнить диапазоны частот, в которых располагаются спектры типичных сигналов в системах связи и вещания:
1) телефонный – 300 ÷ 3400 Гц (стандартный канал тональной частоты),
2) радиовещательный – от 30–50 Гц до 6–15 кГц,
3) телевизионный – 0 ÷ 6 МГц (для вещательного стандарта разложения изображения, принятого в России).
По своей природе различают сигналы детерминированные и случайные. Детерминированные сигналы считаются известными в каждой точке временной оси. В отличие от них значения случайных (стохастических)
сигналов в каждый момент времени являются случайной величиной с той или иной вероятностью. Очевидно, что детерминированные сигналы в силу своей полной определенности не могут нести никакой информации. Их удобно использовать в теории для анализа различных функциональных узлов (ФУ), а на практике в качестве испытательных сигналов для измерения неизвестных параметров и характеристик отдельных звеньев трактов систем связи.
По форме сигналы можно разделить на четыре вида, приведенные в таблице 1.2.
Таблица 1.2.
|
Время t |
|||
|
непрерывное |
дискретное |
||
                        |
Непрерывные |
u(t) аналоговый 1 t |
u(t) 2 t |
|
Дискретные |
  3 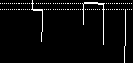 t |
u(t) цифровой 4 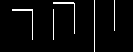  |






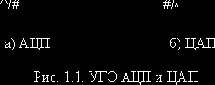 |
Сигнал (1), непрерывный по времени и состояниям, называют аналоговым. Сигнал (4), дискретный по времени и состояниям, – цифровым. Эти сигналы чаще всего используются в различных узлах систем связи. Соответственно различают аналоговые и цифровые ФУ по форме сигналов на их входах и выходах. Возможны преобразования аналогового сигнала в цифровой с помощью аналого-цифрового преобразователя (АЦП) и, наоборот, – с помощью цифро-аналогового преобразователя (ЦАП). Условные графические обозначения (УГО) этих типовых ФУ приведены на рис. 1.1.
Сигналы можно рассматривать в качестве объектов транспортировки по каналам связи и характеризовать основными параметрами, такими как
- длительность сигнала Тс,
- ширина его спектра Fc,
- динамический диапазон



мгновенные мощности сигнала.
Пользуются также более общей характеристикой – объемом сигнала

1.2. Обобщенная структурная схема системы связи
Под системой связи (СС) понимают совокупность технических средств и среды распространения сигнала, служащих для передачи сообщений от источника к получателю.
Обобщенная структурная схема системы связи приведена на рис. 1.2. Она включает только основные ФУ (преобразователи сигналов), необходимые для передачи как дискретных, так и непрерывных сообщений.
Любая система связи начинается с источника, сообщения которого требуется доставить получателю сообщений. В зависимости от вида источника и канала возможны три основных варианта построения систем связи.
Вариант 1. В центральной части рис. 1.2 изображена структура системы передачи дискретных сообщений (СПДС). В нее входят следующие основные ФУ:
1) Кодер источника, служащий, прежде всего, для согласования объемов алфавитов дискретного источника (m>>2) и дискретного канала (m=2). В результате каждый символ источника преобразуется в k-разрядную двоичную комбинацию из 0 и 1. Очевидно, что

2)





































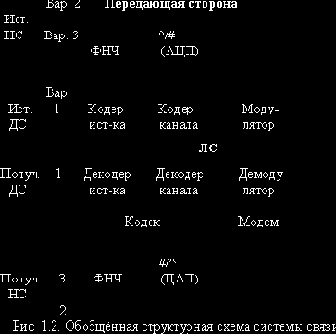
Кодер канала, используемый для повышения помехоустойчивости связи. В нём к входным (информационным) кодовым комбинациям добавляются дополнительные символы, называемые проверочными, которые вместе с правилом их формирования позволяют на приемной стороне обнаруживать и (или) исправлять некоторые из возможных ошибок передачи.
3) Модулятор, служащий для согласования первичного сигнала на выходе кодирующего устройства с характеристиками линии связи. Как правило, это преобразование сводится к преобразованию НЧ сигнала в ВЧ сигнал.
4) Линия связи (ЛС), представляющая собой среду распространения сигнала в части пространства, разделяющего передающую и приемную стороны СС. В ЛС сигнал подвергается искажениям и действию помех.
5) Демодулятор, осуществляющий анализ смеси сигнала с помехой на своем входе в течение времени его существования (временные параметры анализа обеспечиваются системой синхронизации, которая считается идеально работающей и не показана на данной схеме) и на его основе принимающий решение (возможно ошибочное) о том, какой вариант сигнала (из известного множества на входе модулятора) передавался.
В результате на выход выдается «чистая» копия этого сигнала, но уже на следующем тактовом интервале.
6) Декодер канала, обнаруживающий и (или) исправляющий некоторые ошибки во входных кодовых комбинациях, вызванные действием помех в ЛС, по известному ему правилу формирования проверочных символов в кодере канала.
7) Декодер источника преобразующий информационную часть кодовой комбинации в первичное сообщение (символ источника дискретных сообщений) при не обнаружении ошибок передачи.
Совокупность кодера и декодера, выполненных в виде самостоятельного ФУ, называют кодеком, а пару модулятор и демодулятор – модемом.
В тех случаях, кода сообщения по своей природе являются непрерывными (речь, музыка, видео и т.п.), а первичные сигналы соответственно аналоговыми, возможны два варианта их передачи.
Вариант 2. Передача аналогового сигнала непосредственно по ЛС, если она пропускает первичный сигнал с допустимым качеством (городская телефонная сеть), либо с использованием модулятора, реализующего прежнюю функцию согласования сигнала с ЛС. При этом несколько меняется функция демодулятора на приемной стороне, который в этой ситуации обычно называют детектором. Его задача теперь заключается в наиболее точном воспроизведении формы первичного сигнала в результате обработки принятого колебания.
Вариант 3. Передача аналогового сигнала по цифровому каналу связи. В этом случае на передающей стороне возникает необходимость преобразования аналогового первичного сигнала в цифровой с помощью АЦП (функция ФНЧ, ограничивающая спектр сигнала на входе АЦП, станет ясной при изучении в дальнейшем теоремы отсчётов). На приемной стороне полученные после декодирования числовые значения отсчётов с помощью ЦАП преобразуются в соответствующие уровни напряжения и после сглаживания в ФНЧ поступают к получателю в аналоговой форме.
Классификация систем связи
По виду передаваемых сообщений различают:
1) телеграфию (передача текста),
2) телефонию (передача речи),
3) фототелеграфию (передача неподвижных изображений),
4) телевидение (передача подвижных изображений),
5) телеметрию (передача результатов измерений),
6) телеуправление (передача управляющих команд),
7) передачу данных (в вычислительных системах и АСУ).
По диапазону частот – в соответствии с декадным делением диапазонов электромагнитных волн от мириаметровых (3÷30) кГц до децимиллиметровых (300÷3000) ГГц.
По назначению – вещательные (высококачественная передача речи, музыки, видео от малого числа источников сообщений большому количеству их получателей) и профессиональные (связные), в которых число источников и получателей сообщений одного порядка.
Различают следующие режимы работы СС:
1) симплексный (передача сигналов в одном направлении),
2) дуплексный (одновременная передача сигналов в прямом и обратном направлениях),
3) полудуплексный (поочередная передача сигналов в прямом и обратном направлениях).
Уточним уже использованный нами термин канал связи. Под ним принято понимать часть СС между точками А на передающей и Б на приемной сторонах. В зависимости от выбора этих точек, иначе говоря, по виду сигналов на входе и выходе различают каналы:
1) непрерывные,
2) дискретные,
3) дискретно-непрерывные,
4) непрерывно-дискретные.
Каналы связи можно характеризовать по аналогии с сигналами следующими тремя параметрами:
– временем доступа

– шириной полосы пропускания

– динамическим диапазоном

где

сигнала в канале,

Обобщенным параметром канала является его емкость

Очевидным необходимым условием согласования сигнала и канала является выполнение неравенства Vc < Vк .
Менее очевидно то, что это условие является также достаточным и вовсе не обязательно добиваться аналогичного согласования по частным параметрам (длительности, спектру, динамическому диапазону), так как возможен «обмен» ширины спектра сигнала на его длительность или динамический диапазон.
Контрольные вопросы
1. Дайте определения понятиям информация, сообщение сигнал. Какие между ними связи и различия?
2. Приведите примеры сообщений разной физической природы и соответствующих им датчиков сигналов.
3. Каким образом сообщения, описываемые многомерными функциями, преобразуются в сигналы? Приведите примеры.
4. Классифицируйте сигналы по особенностям их формы и спектра.
5. По какому признаку различают НЧ и ВЧ сигналы?
6. По какому критерию различают аналоговые и цифровые сигналы и ФУ?
7. Укажите основные параметры сигналов.
8. Нарисуйте структурные схемы систем связи для:
- передачи дискретных сообщений,
- передачи непрерывных сообщений,
- передачи непрерывных сообщения по цифровым каналам.
- кодера источника и кодера канала,
- модулятора,
- демодулятора,
- декодера канала и декодера источника.
11. Какие системы связи Вам известны:
- по виду передаваемых сообщений,
- по диапазону используемых частот,
- по назначению,
- по режимам работы?
13. Укажите основные параметры каналов связи.
14. Сформулируйте условия согласования сигналов и каналов связи.
Рекомендации по проведению экспериментальных исследований сигналов в системах связи
 |
Рис. 1.3. Некоторые сигналы и их спектры в системе ПДС |
Рекомендуется по результатам наблюдения сигналов в разных точках тракта СПДС провести их классификацию, определить их основные параметры, а также выделить в СПДС разные типы каналов (непрерывный, дискретный, дискретно-непрерывный и непрерывно-дискретный). Полезно также получение наглядного представления о функции каждого ФУ СПДС.
Для закрепления полученных сведений о различии НЧ и ВЧ сигналов и наполнения их практическим содержанием целесообразно провести исследования в рамках лабораторной работы № 4 «Модулированные сигналы». Выбирая в качестве первичных НЧ сигналы разных форм, обратите внимание не только на различие осциллограмм и спектрограмм первичных (НЧ) и модулированных (ВЧ) сигналов, но и на объединяющие их признаки при использовании разных видов модуляции (рис. 1.4).
При выполнении указанных работ не обязательно строго придерживаться имеющихся в них заданий. Используйте возможности ресурсов ВЛ для проведения исследований по своему усмотрению и желанию.
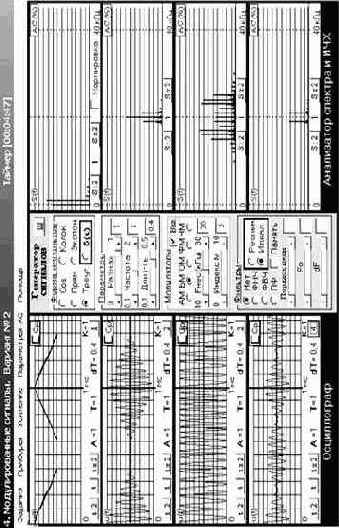 |
Рис. 1.4. Некоторые сигналы и их спектры |
2. Математические модели сигналов
2.1. Сигналы как элементы функциональных
пространств
Сигналы – это, прежде всего, процессы, т.е. функции времени x(t), существующие на ограниченном интервале Т (в теории возможно Т > ?). Их можно изобразить графически (рис. 2.1) и описывать упорядоченной последовательностью значений в отдельные моменты времени tk

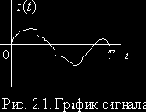
В математике под пространством понимают множество объектов (любой физической природы), наделенных некоторым общим свойством. Свойства, которыми целесообразно наделять пространства сигналов, должны отражать наиболее существенные свойства реальных сигналов, такие как их длительность, энергия, мощность и т.п.
Метрические пространства
Первое свойство, которым мы наделим пространство сигналов, называют метрикой.
Метрическое пространство – это множество с подходящим образом определенным расстоянием между его элементами. Само это расстояние, как и способ его определения, называют метрикой и обозначают



1)


2)

3)

Следует отметить, что метрики можно задать разными способами и в результате для одних и тех же элементов получить разные пространства.
Примеры метрик:
1)

2)

3)

Линейные пространства
Усовершенствуем структуру пространства сигналов, наделив его простыми алгебраическими свойствами, присущими реальным сигналам, которые можно алгебраически складывать и умножать на числа.
Линейным пространством L над полем F называют множество элементов



1. Замкнутость операций сложения и умножения на скаляр:


2. Свойства сложения:


3. Свойства умножения на скаляр:



4.

5.

воположного вектора.
Вектор, образованный суммированием нескольких векторов со скалярными коэффициентами

называют линейной комбинацией (многообразием). Легко видеть, что множество всех линейных комбинаций векторов



Множество векторов называют линейно независимыми, если равенство

возможно лишь при всех ai = 0. Например, на плоскости любые два неколлинеарные вектора (не лежащие на одной прямой) являются линейно независимыми.
Система линейно независимых и ненулевых векторов


Этот единственный набор скаляров {ai}, соответствующий конкретному вектору


Благодаря введению базиса операции над векторами превращаются в операции над числами (координатами)

Если в линейном пространстве L можно отыскать n линейно независимых векторов, а любые n + 1 векторов зависимы, то n – размерность пространства L (dim L = n).
Нормированные пространства
Следующий наш шаг в совершенствовании структуры пространства сигналов – объединение геометрических (характерных для метрических пространств) и алгебраических (для линейных пространств) свойств путем введения действительного числа, характеризующего «размер» элемента в пространстве. Такое число называют нормой вектора и обозначают

В качестве нормы можно использовать любое отображение линейного пространства на действительную ось, удовлетворяющее следующим аксиомам:
1)


2)

3)

Пространства со скалярным произведением
Введем еще одну дополнительную геометрическую характеристику (операцию) в пространстве сигналов в виде отображения упорядоченной пары векторов на поле скаляров из F. Эту операцию называют скалярным (внутренним) произведением векторов и записывают в виде


Скалярное произведение должно удовлетворять следующей системе аксиом (над полем комплексных чисел):
1)

2)

3)


4)


Из этих аксиом следует, что

Если




Если


В линейном пространстве со скалярным произведением целесообразно норму и метрику определять через скалярное произведение


Весьма важное значение имеет соотношение, называемое неравенством Коши-Буняковского-Шварца

На основе скалярного произведения можно ввести понятие угла j между двумя векторами, исходя из соотношения

В ТЭС наибольший практический интерес представляют следующие линейные нормированные метрические пространства:
1. Rn – n-мерное вещественное евклидово пространство, в котором каждый вектор определяется совокупностью n его координат


Оно порождает норму и расстояние


2. L2(T) – бесконечномерные пространства (Гильберта), которое образуют непрерывные комплексные

Скалярное произведение векторов в этом пространстве

Квадрат нормы

имеет ясный физический смысл энергии Ех сигнала, если под x(t) иметь в виду напряжение (или ток) на сопротивлении 1 Ом. Квадрат расстояния между вещественными сигналами x(t) и y(t) определяется соотношением

и имеет смысл энергии разностного сигнала.
3. L2(?) – бесконечномерные пространства (Гильберта), которое образуют непрерывные комплексные



не выполняется, но выполняется условие ограничения мощности

то можно ввести скалярное произведение векторов в этом пространстве с размерностью мощности

и норму

4. 2n – n-мерное пространство Хэмминга, которые образуют двоичные n-последовательности (кодовые комбинации из 0 и 1), широко используемые в системах ПДС. Норму и метрику в этом пространстве задают в виде


где знак Å обозначает операцию сложения по модулю 2 (по правилам: 0 Å 0 = 0, 0 Å 1 = 1, 1 Å 0 = 1, 1 Å 1 = 0).
Таким образом, норма вектора в пространстве Хэмминга определяется общим количеством содержащихся в нем единиц, а расстояние между двоичными векторами – количеством позиций (разрядов) кодовых комбинаций, в которых они различаются.
Следует отметить, что вещественные пространства Rn (при n > ?), L2(T) и L2(?) изоморфны (эквивалентны). Это означает, что между их элементами (равно как суммами элементов, их произведениями на скаляры и скалярными произведениями) можно установить взаимно-однозначное соответствие. Изоморфны также соответствующие им комплексные пространства. Понятие изоморфизма имеет большое практическое значение, так как позволяет представить одну модель сигнала другой.
2.2. Разложение сигналов в обобщенный ряд Фурье
Введем в пространстве L2(T) базис {?i(t)}. Для упрощения последующих вычислений будем полагать, что он ортонормированный, т.е. отвечает условию

Тогда любую функцию х(t) из L2(T) можно представить через проекции Ci вектора


Для нахождения проекций Cj, называемых также коэффициентами разложения х(t) в обобщенный ряд Фурье, вычислим скалярное произведение


Таким образом

Получим еще одно важное соотношение

Контрольные вопросы
1. Что понимают под «пространством сигналов»?
2. Какие пространства называют метрическими?
3. Что такое «метрика» пространства и каким требованиям она должна удовлетворять?
4. Какие пространства называют линейными?
5. Сформулируйте аксиомы линейного пространства.
6. Каковы условия линейной независимости векторов?
7. Что такое «линейная оболочка» векторов

8. Что такое «базис» в пространстве L?
9. Что называют координатами (проекциями) вектора по заданному базису?
10. Какие пространства называют нормированными?
11. Что представляет собой норма вектора и каким требованиям она должна удовлетворять?
12. Какой физический смысл имеет норма сигнала в пространствах L2(T) и L2(¥)?
13. Что представляет собой скалярное произведение векторов и какими свойствами оно обладает?
14. Как определяют «угол» между векторами (сигналами)?
15. Приведите примеры пространств со скалярным произведением. Как оно вычисляется в этих пространствах?
16. Как скалярное произведение порождает норму и метрику?
17. Что называют обобщённым рядом Фурье?
18. Как вычисляют коэффициенты разложения в обобщённый ряд Фурье?
19.
Напишите равенство Парсеваля и дайте ему физическую трактовку.
2.3. Спектральное представление сигналов
Спектры периодических сигналов
Периодическими называют сигналы, обладающие следующим свойством
x(t) = x(t – kT), где Т – период, k = 0, ±1, ±2, ±3,… .
Как известно, такие функции (если они удовлетворяют известным из математики условиям Дирихле, которые для интересующих нас случаев всегда выполняются) можно представить суммой тригонометрического ряда (ряда Фурье)

где



Форма (2. 1) ряда Фурье удобна с точки зрения простоты вычисления коэффициентов разложения ak и bk . Ряд Фурье можно записать иначе

где




Совокупность амплитуд Ak называют амплитудным, а совокупность фаз jk – фазовым спектрами. Их можно изображать графически (рис. 2.1). Амплитудный и фазовый спектры сигнала в совокупности однозначно определяют его форму (временную зависимость).
       
0 F1 2F1 3F1 4F1 5F1 6F1 7F1 f    
   j2 j5 Рис. 2.1. Амплитудный и фазовый спектры |
Наиболее компактной является запись ряда Фурье в комплексной форме

где

Комплексный спектр (2.4) можно интерпретировать как представление x(t) в виде сумм спектральных составляющих




Сопоставляя (2.2) и (2.4) с (2.1), нетрудно убедиться, что ряд Фурье является частным случаем обобщённого ряда Фурье при выборе в качестве базиса совокупности тригонометрических


Выводы
1. Математическим аппаратом спектрального анализа периодических сигналов являются ряды Фурье.
2. Спектры периодических сигналов дискретные (линейчатые), представляют собой совокупность амплитуд и фаз гармонических колебаний (составляющих) следующих по оси частот через интервалы ?f = f1 = 1/T.
3. Ряд Фурье является частным случаем обобщенного ряда Фурье при использовании в качестве базиса


Спектры Т-финитных сигналов
Т-финитными называют ограниченные по времени сигналы. По определению они не могут быть периодическими и, следовательно, к ним не применимо разложение в ряды Фурье.
Чтобы получить адекватное описание таких сигналов в частотной области используют следующий прием. На первом этапе от заданного сигнала x(t), имеющего начало в точке t1 и конец в точке t2 переходят к сигналу xп(t), являющемуся периодическим повторением x(t) на бесконечной оси времени с периодом


где

Введём в рассмотрение текущую частоту


Тогда

Исходный сигнал x(t) можно получить из xп(t) в результате предельного перехода Т® ¥ .
При этом








В данном случае (и в дальнейшем) комплексную функцию


Из полученных соотношений следует, что спектр Т-фи- нитного сигнала сплошной. Он представляет собой совокупность бесконечного числа спектральных составляющих с бесконечно малыми амплитудами


где


Выводы
1. Математическим аппаратом спектрального анализа Т-финитных сигналов является интегральное преобразование Фурье.
2. Спектры Т-финитных сигналов сплошные и описываются непрерывными функциями частоты в виде модуля спектральной плотности амплитуд


Свойства преобразования Фурье
1. Прямое и обратное преобразование Фурье являются линейными операторами, следовательно, действует принцип суперпозиции. Если


2. Прямое и обратное преобразование Фурье являются взаимно однозначными.
3. Свойство запаздывания.
Если



(в данном случае использованы подстановки:



4. Спектральная функция ?-функции.
Используя общее выражение спектральной функции и фильтрующее свойство ?-функции, получим

5. Спектральная функция комплексного гармонического сигнала


Используя одно из определений ?-функции

и выполняя в нём взаимную замену t и w (или f), получим


Сопоставляя полученный результат с (2.5), имеем

6. Скалярное произведение комплексных сигналов в спектральной области. Пусть


Их скалярное произведение


Из полученного результата для вещественных функций



где


а

Для сигналов x(t), заданных на бесконечной оси времени (–¥,+¥), с




Тогда




7. Скалярное произведение комплексных сигналов




При





– корреляционная функция сигнала x(t).
Из последнего выражения вытекают важные соотношения между корреляционной функцией и энергетическим спектром сигнала



8. Спектр произведения сигналов








Таким образом, спектральная функция произведения двух сигналов является свёрткой их спектральных функций.
Справедливо также и обратное соотношение

9. Свойство смещения спектра.
Если



10. Ширина спектра.
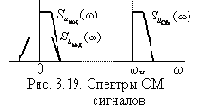
Теоретически ширина спектра сигналов бесконечна. Однако, учитывая, что интенсивность спектральных составляющих реальных сигналов уменьшается с ростом их частоты (не обязательно монотонно), можно ввести понятие практической (конечной) ширины спектров (рис. 2.3 и 2.4). Практическую ширину спектра DW можно определять как ширину частотного интервала, в пределах которого амплитудный спектр S(w) не меньше некоторого условного уровня g (например g = 0,1) от S(w)max или энергия (мощность) сигнала составляет определённую часть g (например g = 0,9) от полной

Для импульсов простых форм (прямоугольной, треугольной и т.п.), спектральная функция которых периодически принимает нулевые значения с ростом частоты (рис. 2.3 и 2.4), практическую ширину спектра часто определяют по первому или второму или иному «нулю» амплитудного спектра.
Независимо от способа определения практической ширины спектра Т-финитного сигнала выполняется общая закономерность – произведение практической ширины спектра на длительность сигнала Dt есть константа C, зависящая только от формы импульса
DW·Dt = C.
Это соотношение имеет фундаментальное значение в теории связи.
Из него вытекает, что чем короче сигнал, тем шире его спектр и, следовательно, тем более широкополосный канал требуется для его передачи.
Контрольные вопросы
1. Какие сигналы являются периодическими?
2. Какой математический аппарат используется для спектрального анализа периодических сигналов?
3. Что называют амплитудным и фазовым спектрами периодического сигнала?
4. Какими свойствами обладают спектры периодических сигналов?
5. Как вычисляют амплитуды и фазы спектральных составляющих периодических сигналов?
6. Какие сигналы называют Т-финитными?
7. Какой математический аппарат используется для спектрального анализа Т-финитных сигналов?
8. Что такое спектральная функция (спектральная плотность амплитуд) сигнала и какова её размерность?
9. Что понимают под амплитудным и фазовым спектрами Т-финитного сигнала?
10. Как изменяется спектр сигнала в результате его задержки на время t?
11. Что представляет собой спектр d-функции?
12. Какова спектральная функция гармонического колебания?
13. Как можно вычислить скалярное произведение сигналов в спектральной области?
14. Что представляют собой спектральные плотности энергии и мощности сигналов? Каковы их размерности и свойства?
15. Что представляет собой корреляционная функция сигнала

16. Как вычисляют спектр произведения сигналов?
17. Как изменяется спектр сигнала в результате его умножения на гармоническое колебание?
Рекомендации по проведению экспериментальных исследований ортогональности и спектров сигналов
Для закрепления полученных в разделе 2.1 знаний полезно провести экспериментальные исследования на базе лабораторной работы № 5 «Ортогональность сигналов» (из перечня тем виртуальной учебной лаборатории) в полном объёме (рис. 2.2). Она позволяет понять, как на практике реализуется вычисление скалярного произведения двух сигналов, экспериментально определить являются ли выбранные пары сигналов ортогональными на установленном временном интервале.
Обратите внимание на условия ортогональности двух гармонических сигналов разных частот и их связь с интервалом ортогональности.
Для закрепления полученных в разделе 2.3 знаний по спектральному представлению периодических сигналов полезно выполнить лабораторную работу № 1 «Сигналы и спектры» в полном объёме, а также провести дополнительные экспериментальные исследования, используя иные виды сигналов в рамках предоставляемых этой работы ресурсов (рис. 2.3). Обратите внимание на дискретность спектров и связи их характеристик с параметрами и формой сигналов.
Для закрепления полученных в разделе 2.3 знаний по спектральному представлению финитных сигналов полезно на базе лабораторной работы № 22 «Согласованная фильтрация сигналов известной формы» провести экспериментальные исследования спектров одиночных импульсов разных форм, используя генератор сигналов, предоставляемый этой работой (рис. 2.4). Обратите внимание на сплошной характер спектров одиночных импульсов и на их связь с формой импульсов.
При выполнении указанных работ не обязательно строго придерживаться имеющихся в них заданий. Используйте возможности ресурсов ВЛ для проведения исследований по своему усмотрению и желанию.
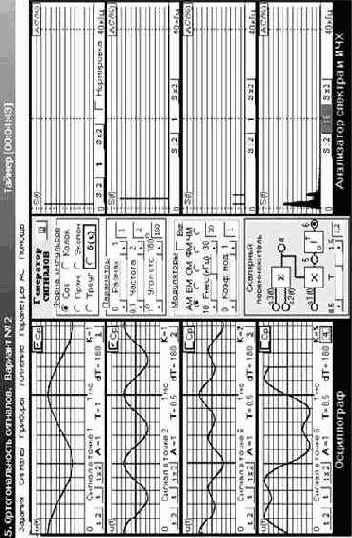 |
Рис. 2.2. Исследование ортогональности сигналов |
 |
Рис. 2.3. Спектры некоторых периодическихъ сигналов |
 |
Рис. 2.4. Спектры некоторых Т-финитных сигналов |
Под дискретизацией сигналов (в узком смысле) понимают преобразование аналогового сигнала x(t) в последовательность отсчётов его мгновенных значений, взятых через интервалы времени Dt (рис. 2.5)

Dt – шаг дискретизации,

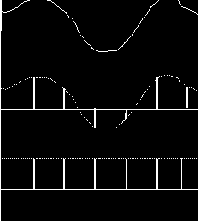 а t xд(t) б t yр(t) 1 в t Рис. 2.5. Дискретизация сигнала |


где

Функция


Введение функции


Как и d-функция


Поскольку



и, следовательно,

Учитывая свойство спектральной функции комплексного гармонического колебания (2.6) и выражение (2.8), имеем


Исходя из очевидных соотношений


Окончательно

и по свойству смещения спектра (2.7)

Из (2.10) вытекает, что процесс дискретизации сигналов можно реализовать на перемножителе (рис.2.6).






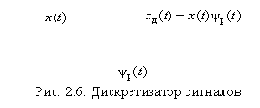 |
Дискретизация сигналов широко используется в системах связи. Она является необходимой операцией при передаче аналоговых сигналов по цифровым каналам (для преобразования аналогового сигнала в цифровой поток его отсчётов) и в системах многоканальной передачи с временным уплотнением (для разделения заданного множества аналоговых сигналов во временной области). Во всех этих случаях важнейшими являются вопросы о выборе частоты дискретизации сигналов, способе их восстановления (обратного преобразования отсчётов в аналоговый сигнал) и степени искажений в процессе таких преобразований. Ответы на эти вопросы даёт теорема отсчётов (часто называемая именем Котельникова В.А. – автора одного из её доказательств в 1933 г.).
Теорема отсчётов
Любой F-финитный сигнал (сигнал с ограниченным частотой Fв спектром) точно определяется последовательностью своих отсчётов, взятых через интервалы

Справедливость этого утверждения следует из рассмотрения спектров, приведённых на рис. 2.7. На рис. 2.7(а) изображён двусторонний спектр исходного аналогового сигнала







Исходя из свойства взаимно однозначного соответствия



1) фильтрацией дискретизированного сигнала с помощью идеального ФНЧ с частотой верхнего среза

2) только в случае

Таким образом, процедура восстановления сигнала по

отсчётам может быть осуществлена идеальным ФНЧ с передаточной функцией


и, соответственно, с импульсной характеристикой

Поскольку импульсная характеристика цепи есть её реакция на воздействие в виде d-функции







На практике абсолютно точное восстановление сигналов по их отсчётам невозможно по следующим причинам:
1) Идеальный ФНЧ – физически нереализуемая цепь, т.к. его импульсная характеристика отлична от 0 при t<0. Характеристики реальных ФНЧ могут быть приближены к идеальным лишь с определенной погрешностью, тем меньшей, чем больше задержка.
2) Реальные сигналы являются Т-финитными, а следовательно имеют неограниченный по частоте спектр. Если всё же спектр сигнала ограничить частотой


где

При осуществлении дискретизации сигнала, когда частота дискретизации


Контрольные вопросы
1. В чём заключается операция дискретизации непрерывных сигналов? Как её записать математически?
2. Как изменяется спектр сигнала в результате его дискретизации?
3. Приведите примеры практического использования дискретизации сигналов в системах связи.
4. Сформулируйте теорему отсчётов. В чём состоит её фундаментальное значение?
5. Из каких соображений выбирается частота дискретизации непрерывных сигналов?
6. Каким образом и каким ФУ обеспечивается восстановление непрерывного сигнала по его отсчётам?
7. Укажите причины погрешностей восстановления непрерывных сигналов по их отсчётам.
8. Напишите выражение сигнала в виде ряда Котельникова.
9. Какой базис используется при разложении сигналов в ряд Котельникова?
10. Как определяются коэффициенты разложения сигналов в ряд Котельникова?
11. Объясните необходимость использования антиэлайсингового фильтра при дискретизации сигналов.
12. Приведите примеры проявления искажений, связанных с наложением спектров сигнала после его дискретизации (при

Рекомендации по проведению экспериментальных исследований дискретизации и восстановления сигналов
Для закрепления полученных в разделе 2. 4 знаний полезно выполнить лабораторную работу № 3 «Дискретизация и восстановление сигналов» (из перечня тем виртуальной учебной лаборатории) в полном объёме, а также провести дополнительные экспериментальные исследования, используя иные виды сигналов в рамках предоставляемых этой работы ресурсов (рис. 2.8). Обратите особое внимание на характер изменения спектра сигнала при его дискретизации, на его зависимость от частоты дискретизации, а также на связь точности восстановления сигналов по их отсчётам с качеством и параметрами фильтров-восстановителей. Выясните, как влияет наличие (отсутствие) схемы выборки-хранения (СВХ) в составе дискретизатора на форму и спектр дискретизированного сигнала.
 |
Рис. 2.8. Исслежование дискретизации и восстановления сигналов |
Во многих случаях сигнал


где




Для определения









Поскольку сопряженный


По ряду причин, часть из которых станет понятной из дальнейшего, в качестве сопряжённого удобно выбрать преобразованный по Гильберту исходный сигнал

Комплексный сигнал вида

Преобразование Гильберта










или

где

Найдём импульсную характеристику преобразователя Гильберта


Первый интеграл в полученном выражении равен 0 в силу интегрирования нечетной функции при симметричных пределах, а второй сводится к табличному интегралу вида


Окончательно получаем

Из полученного результата с очевидностью вытекает невозможность физической реализации преобразования Гильберта, т.к.

Рассмотрим преобразование Гильберта во временной области. Из рис. 2.9 вытекает


Поскольку

то, после умножения обеих частей равенства на


откуда следует, что передаточная функция обратного преобразования Гильберта


Соответственно

– обратное преобразование Гильберта.
Свойства аналитического сигнала
1. Аналитический сигнал является естественным обобщением символического изображения гармонического колебания



2. Спектр аналитического сигнала располагается только в области положительных частот w > 0


3. Сигналы







4. Сдвиг всех спектральных составляющих действительного сигнала



Действительно, если



Таким образом,

Из полученного результата следует возможный алгоритм получения общего фазового сдвига всех спектральных составляющих действительного сигнала вида


5. Преобразование частоты сигнала






Из этого выражения вытекает широко используемый алгоритм преобразования частоты

Представление действительного сигнала x(t)
через его квадратурные компоненты
Любой действительный сигнал





где


квадратурные компоненты сигнала



Представление







Обработку узкополосных сигналов можно выполнить проще и точнее через обработку их квадратурных компонентов. Действительно, если выполняется условие узкополосности сигнала, то спектр комплексного сигнала вида


получаемого сдвигом спектра огибающей




Таким образом, можно считать, что преобразование Гильберта узкополосного сигнала сводится к сдвигу фаз на угол –90° гармонических колебаний









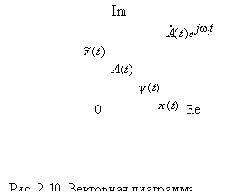

Угловая скорость его вращения изменяется во времени по закону

Контрольные вопросы
1. Как выглядит квазигармоническая форма записи произвольного сигнала

2. Как определяют огибающую, фазу и мгновенную частоту сигнала

3. Почему задача определения огибающей и фазы сигналов не является однозначной?
4. Какой сигнал называют аналитическим?
5. В чём заключается преобразование Гильберта в частотной области?
6. Как схемотехнически реализуют преобразование Гильберта?
7. Напишите выражение передаточной функции преобразователя Гильберта.
8. Какова импульсная характеристика преобразователя Гильберта?
9. Напишите аналитическое выражение преобразования Гильберта во временной области.
10. Чем обратное преобразование Гильберта отличается от прямого?
11. Какая связь аналитического сигнала с символическим изображением гармонического колебания, используемым в символическом методе.
12. Каковы особенности спектра аналитического сигнала?
13. Как изменяется аналитический сигнал при сдвиге фаз всех его спектральных составляющих на один и тот же угол j?
14. Как с помощью аналитического сигнала записать операцию смещения спектра сигнала на Dw?
15. Что называют квадратурными компонентами сигнала?
16. Запишите аналитическое выражение сигнала

17. Как огибающая и фаза сигнала связаны с его квадратурными компонентами?
18. Почему обработку узкополосных сигналов проще и точнее реализуют через их квадратурные компоненты?
19. Что представляет собой векторная диаграмма аналитического сигнала?
Рекомендации по проведению экспериментальных
исследований компонентов аналитического сигнала
Для закрепления полученных в разделе 2.5 знаний по квазигармоническому представлению сигналов целесообразно на базе лабораторной работы № 29 «Аналитический сигнал» провести экспериментальные исследования связи форм и спектров НЧ и ВЧ сигналов х(t) (от генератора сигналов) с их преобразованиями по Гильберту H[х(t)], огибающими A(t), фазой Ф(t), квадратурными косинусной Ac(t) и синусной компонентами As(t) (рис. 2.11). Обратите внимание на существенное различие форм исходного и преобразованного по Гильберту сигналов при полной идентичности их амплитудных спектров. Полезно также наблюдать огибающие ВЧ сигналов с разными видами линейной модуляции (АМ, БМ и ОМ). Попробуйте на основании такого рода наблюдений определить связи огибающих ВЧ сигналов с соответствующими модулирующими НЧ сигналами.
При выполнении указанных работ не обязательно строго придерживаться имеющихся в них заданий. Используйте возможности ресурсов ВЛ для проведения исследований по своему усмотрению и желанию.
3. Преобразования сигналов
в типовых функциональных узлах систем связи
К анализу и синтезу функциональных узлов (ФУ) систем связи можно подходить с позиций «чёрного ящика», имеющего один или несколько входов и выход (рис. 3.1).
Входные сигналы ФУ называют воздействиями, а выходной – реакцией ФУ на воздействия.
 |
Рис. 2.11. Исследование компонентов аналитического сигнала |




который однозначно определяет сам ФУ и который будем называть его функциональной характеристикой. По виду этого оператора производят классификацию ФУ на линейные, параметрические и нелинейные.
В теории цепей приходится решать задачи анализа и синтеза ФУ в зависимости от цели и исходных условий.
В задаче анализа известными считают воздействие


В задаче синтеза в качестве заданных рассматриваются воздействие


Широко используется и смешанный (эвристический) подход, при котором, как и в задаче синтеза, заданными являются воздействие


3.1. Особенности преобразования сигналов
в линейных, параметрических и нелинейных ФУ
Линейные преобразования сигналов и ФУ Линейные ФУ по определению описываются линейными дифференциальными уравнениями (в том числе нулевого порядка для резистивных цепей) с постоянными коэффициентами. С точки зрения схемотехники это значит, что все элементы ФУ (R, C, L) имеют постоянные параметры. Оператором преобразования воздействия x(t) в реакцию y(t) для них может служить одна из форм интеграла наложения (Дюамеля) во временной области

или передаточная функция Н


а в качестве функциональной характеристики линейного ФУ можно использовать его импульсную характеристику


Простым колебанием для линейных цепей является гармоническое

1. Форма сложного сигнала (с полигармоническим или сплошным спектром) при его прохождении через линейную цепь может изменяться только вследствие изменения соотношения между амплитудами и фазами спектральных составляющих воздействия. Принципиально важно, что в реакции линейного ФУ не могут возникнуть спектральные компоненты, отсутствующие в спектре воздействия.
2. Из вывода 1 вытекают возможности построения на основе линейных цепей ограниченного класса типовых ФУ:
а) усилителей и аттенюаторов (ФУ для изменения мощности сигналов без искажения их формы), передаточная функция которых в полосе частот, занимаемой спектром воздействия, имеет вид

б) фильтров разных типов (ФНЧ, ФВЧ, ПФ, РФ, интеграторов, дифференциаторов, фазовращателей и т.п.), передаточная функция которых в полосе частот, занимаемой спектром воздействия, имеет вид

где Н(w) (АЧХ) и j(w) (ФЧХ) – заданные функции частоты.
Параметрические преобразования сигналов и ФУ По определению параметрические ФУ описываются линейными дифференциальными уравнениями (в том числе нулевого порядка для резистивных цепей), у которых есть коэффициенты, зависящие от независимой переменной (времени).








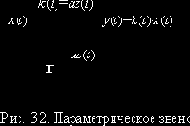
Параметрическое звено ">



где

Рассмотрим реакцию параметрического звена (рис. 3.1) при




Спектры воздействия и реакции приведены на рис. 3.3. Из их рассмотрения можно сделать следующие выводы:
1. Параметрические ФУ обогащают спектр воздействия новыми спектральными составляющими.
2. Частоты новых спектральных составляющих в реакции параметрических ФУ определяются частотами спектральных составляющих воздействия и частотами изменения параметров ФУ.
Нелинейные преобразования сигналов и ФУ Нелинейные преобразователи сигналов описываются нелинейными дифференциальными уравнениями (в том числе нулевого порядка для резистивных цепей), у которых хотя бы один коэффициент зависит от их решения (искомой функции). Соответственно, их схема содержит хотя бы один
         Спектр   Спектр  0 W wс–W wс wс+W w Рис.3.3. Спектры    |







Рассмотрим возможности изменения спектра сигнала при его прохождении через БНП – цепь 0-го порядка. Для таких цепей в теории широко используют два основных метода спектрального анализа реакции в зависимости от вида аппроксимации функциональной характеристики БНП:
1) метод кратных дуг – при полиномиальной аппроксимации

2) метод угла отсечки (коэффициентов Берга) – при кусочно-линейной аппроксимации.
Чтобы воспользоваться первым методом, достаточно помнить тригонометрическую формулу

и её частный случай (при


Результаты анализа спектрального состава реакции БНП с полиномиальной функциональной характеристикой при моно- и бигармоническом воздействии приведены в таблице 3.1. В ней указаны только частоты спектральных составляющих реакции.
Из этой таблицы следует, что БНП обогащает спектр воздействия постоянной составляющей, кратными гармониками и колебаниями комбинационных частот вида




Выводы 1. Нелинейные ФУ обогащают спектр воздействия новыми спектральными компонентами.
2. Новые спектральные компоненты реакции нелинейных ФУ являются гармониками частот воздействия или колебаниями комбинационных частот вида

Таблица 3.1
 |
Спектральный состав  |
|
 |
 |
|
 |
0 |
0 |
 |
w0 |
  |
 |
0, 2w0 |
0, 2w1, 2w2,  |
 |
 |
        |
|
+ … |
||
+ |
0, 2w0, 4w0,…, kw0 при k = 2q,  при k = 2q+1, q = 1, 2, 3,… |
      |
|
+ … |
||
 |
0, 2w0, 4w0,…, nw0 при n = 2q,  при n = 2q+1, q = 1, 2, 3,… |
      |
1. Сформулируйте задачи анализа и синтеза ФУ.
2. Дайте классификацию ФУ по виду описывающих их дифференциальных уравнений.
3. Каковы принципиальные ограничения на возможности преобразования сигналов в линейных ФУ?
4. Что можно использовать в качестве функциональных характеристик линейных ФУ?
5. Какие типовые ФУ, используемые в системах связи, можно реализовать в классе линейных цепей?
6. Каковы возможности параметрических ФУ по преобразованию сигналов?
7. Опишите характер обогащения спектров сигналов в параметрических ФУ.
8. Каковы возможности нелинейных ФУ по преобразованию сигналов?
9. Какие виды аппроксимации функциональных характеристик безынерционных нелинейных преобразователей целесообразны в режимах а) слабого сигнала, б) сильного сигнала?
 |
Рис. 3.5. Исследование преобразований сигналов в линейных ФУ |
11. Какой метод спектрального анализа реакции нелинейного ФУ используют при кусочно-линейной аппроксимации его функциональной характеристики?
12. Опишите спектральный состав реакции нелинейного ФУ на моногармоническое воздействие.
13. Опишите спектральный состав реакции нелинейного ФУ на полигармоническое воздействие.
14. Нарисуйте схему перемножителя сигналов и укажите назначение её элементов.
15. При каких условиях кольцевой диодный перемножитель обеспечивает «чистое» перемножение сигналов?
16. В чём сущность метода фазовой компенсации побочных продуктов нелинейного преобразования сигналов?
Рекомендации по проведению экспериментальных исследований преобразований сигналов в линейных, нелинейных и параметрических ФУ
Для закрепления полученных в разделе 3.1 знаний полезно выполнить лабораторные работы № 2 «Линейная фильтрация сигналов» (рис. 3.5), № 6 «Преобразования сигналов в нелинейных цепях» (рис. 3.6) и № 7 «Нелинейное усиление и умножение частоты сигналов» (из перечня тем виртуальной учебной лаборатории) (рис. 3.7) в полных объёмах, а также провести дополнительные экспериментальные исследования, используя иные виды сигналов в рамках предоставляемых этими работами ресурсов. Обратите, прежде всего, внимание на принципиальные различия в характере трансформации спектров входных сигналов в результате их линейных и нелинейных преобразований. Сформулируйте, в чём состоят эти отличия и какие практически важные следствия они имеют с точки зрения реализации ФУ раз-
 |
Рис. 3.6. Исследование преобразований сигналов в нелинейных ФУ |
|
|
 |
Рис. 3.7. Исследование преобразований сигналов в нелинейных ФУ |
Для экспериментальных исследований параметрических преобразований сигналов можно воспользоваться параметрическими преобразователями, входящими в состав системы передачи непрерывных сообщений из лабораторной работы № 11 «Линейные виды модуляции и синхронное детектирование» (рис. 3.8). В рамках ресурсов, предоставляемых этой работой, можно провести наблюдение осциллограмм и спектрограмм произведения произвольного сигнала s1(t) с гармоническим колебанием. В качестве произвольного входного сигнала s1(t) используйте как НЧ, так и ВЧ сигналы, выбирая их с помощью пункта меню «Сигналы/ s1(t)» этой работы. Обратите внимание на характер обогащения спектра параметрическим преобразователем и определите частоты новых спектральных составляющих на его выходе.
3.2. Перемножение сигналов






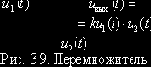

































Кольцевой диодный перемножитель сигналов ">
1) все диоды имеют квадратичные вольтамперные характеристики (режим слабого сигнала)

с одинаковыми коэффициентами

2) сопротивления нагрузочных резисторов R одинаковы (симметрия схемы),
3) один из входных сигналов поступает от двух идентичных источников (e1) (симметрия схемы).
Выходное напряжение


Для определения токов диодов подставим в выражение их вольтамперной характеристики соответствующие напряжения



+

–

–




Обратим внимание на то, что





Выводы
1. ФУ (рис. 3.10) является «чистым» перемножителем произвольных сигналов


2. «Чистота» операции перемножения достигнута методом фазовой компенсации.
3. Суть метода фазовой компенсации заключается в следующем:
- ФУ строится по симметричной многоканальной схеме,
- выходные реакции каналов суммируются,
- на входы каналов сигналы подают с таким подбором фаз, чтобы при сложении реакций каналов полезные составляющие оказались бы синфазными и суммировались, а побочные были бы противофазными и взаимно компенсировались.
3.3. Амплитудная модуляция
Модуляция в системах связи используется тогда, когда непосредственная передача первичного сигнала по линии связи оказывается невозможной. Согласование передаваемого сигнала с характеристиками линии связи достигается использованием колебания, которое хорошо распространяется в имеющейся линии связи. Один или несколько параметров этого колебания связывают с первичным сигналом. Такое колебание называют переносчиком, процесс изменения его параметра(ов) – модуляцией, первичный сигнал – модулирующим, а получаемый вторичный сигнал – модулированным.
В качестве переносчика широко применяют гармоническое несущее колебание



Добавление к модулирующему сигналу




Спектры АМ сигналов
1. Спектр простого АМ сигнала.
Модулированный сигнал называют простым, если в качестве модулирующего сигнала



где Uн – амплитуда несущего колебания,
m – коэффициент (глубина) модуляции,

Для получения спектра сигнала простого АМ сигнала достаточно в выражении (3.2) раскрыть скобки


Таким образом, спектр простого АМ сигнала содержит несущее и два боковых колебания (рис.3.11). Нетрудно видеть, что его ширина


        
0 wн w   Uн     DwАМ 0 W wн–W wн wн+W w Рис.3.11. Спектры    |
На основе выражения (3.2) спектр сложного АМ сигнала при полигармоническом модулирующем сигнале можно записать в виде

где W1, W2 ,… – частоты модулирующего сигнала,
m1, m2,… – парциальные коэффициенты модуляции.
В случае Т-финитного модулирующего сигнала соответствующий АМ сигнал выглядит следующим образом


где kАМ – нормирующий коэффициент, обеспечивающий условие A(t)?0.
Для нахождения его спектральной функции перейдём к комплексному сигналу

Используя свойства преобразования Фурье (2.6) и (2.7), получим






































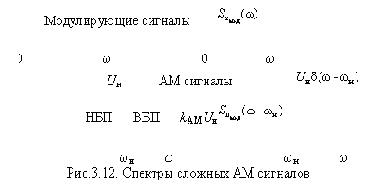
Выводы 1. Спектр АМ сигнала содержит: а) несущее колебание на частоте wн,
б) верхнюю боковую полосу (ВБП), представляющую собой спектр модулирующего сигнала

в) нижнюю боковую полосу (НБП), являющуюся «зеркальным отражением» ВБП относительно wн.
2. Ширина спектра АМ сигнала вдвое больше максимальной модулирующей частоты


где

Максимальная (пиковая) мощность, на которую рассчитывают усилители АМ сигналов,

до 4 раз превышает мощность

Средняя мощность АМ сигнала за период модулирующего сигнала (потребляемая от источников питания модулятора или усилителя АМ сигнала)

где

Из полученных результатов можно сделать вывод о низкой энергетической эффективности амплитудной модуляции, так как полезная (в информационном смысле) мощность боковых колебаний



Векторная диаграмма простого АМ сигнала












Векторная диаграмма простого АМ сигнала ">

Построение амплитудных модуляторов





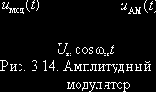










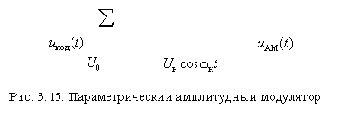
|
+ E0 С L Ср i VT uвых e1 e2 Есм uвх Рис. 3.16. Амплитудный модулятор |
Выходной ток i транзистора VT, который должен работать в нелинейном режиме, обогащается новыми спектральными компонентами, среди которых кроме полезных (боковых – комбинационных колебаний суммарной и разностной частот е1 и е2) много побочных (помех). Последние устраняются из спектра выходного напряжения uвых благодаря избирательной нагрузке – LC контуру, настроенному на несущую частоту

Полоса пропускания контура




Для определения оптимального режима модулятора пользуются статической модуляционной характеристикой (СМХ)


где I1 – амплитуда первой гармоники тока частоты















- оптимальное напряжение смещения

- максимальную амплитуду модулирующего сигнала ЕW макс,
- среднюю амплитуду первой гармоники тока I1 ср,
- максимальное изменение амплитуды первой гармоники тока DI1,
- оптимальный коэффициент модуляции

3.4. Другие виды линейной модуляции (БМ, ОМ, КАМ)
Амплитудная модуляция относится к линейным видам модуляции вследствие линейной зависимости модулированного сигнала от модулирующего (3.1). Выше отмечалась её низкая энергетическая эффективность. Первое очевидное решение для преодоления этого недостатка заключается в исключении из спектра АМ сигнала несущего колебания. В результате приходим к двухполосной передаче с подавленной несущей. Получение такого двухполосного сигнала весьма просто – достаточно из модулирующего сигнала исключить постоянную составляющую (если она есть), используя, например, разделительный конденсатор Ср и умножить его на несущее колебание (рис. 3.18).










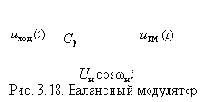

причём в моменты смен знака

Как отмечалось выше при рассмотрении спектра АМ сигнала, нижняя боковая полоса является «зеркальным отражением» верхней, т.е. не содержит никакой дополнительной информации о модулирующем сигнале. Отсюда возникает возможность передачи сигналов с помощью однополосной модуляции (ОМ). При этом безразлично какую из двух полос ВБП или НБП использовать при однополосной передаче.
ОМ сигнал можно получать из БМ сигнала фильтровым или фазокомпенсационным методами. Фильтровой метод в силу своей очевидности не требует дополнительных пояснений. Отметим лишь высокие требования к крутизне ската АЧХ полосового фильтра для выделения ВБП или НБП (по причине малого «частотного зазора» 2Wмин между ними), возрастающие с увеличением несущей частоты.
Синтезируем однополосный модулятор на основе фазокомпенсационного метода подавления одной из боковых полос. Для этого обратимся к аналитическому модулирующему сигналу





Вернёмся к действительному ОМ сигналу





















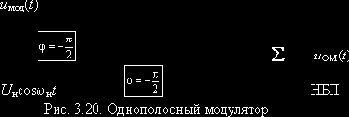
Однополосный модулятор ">
Самостоятельно убедитесь в том, что для получения НБП достаточно в выражении (3.6) разность заменить на сумму.
Подставим в (3.6) модулирующий сигнал в квазигармонической форме



Из полученного результата видно, что в результате однополосной модуляции сохраняется огибающая модулирующего сигнала, а мгновенная частота возрастает на wн

Однополосную модуляцию можно рассматривать как самую простую – перенос (транспонирование) спектра модулирующего сигнала с сохранением его огибающей, а можно как сложную – амплитудную и фазовую одновременно. Она является самой узкополосной – ширина спектров модулирующего и однополосного сигналов одна и та же. Важным преимуществом ОМ по сравнению с АМ является энергетический выигрыш, доходящий (в зависимости от статистики модулирующего сигнала) до 10 раз.
К недостаткам ОМ можно отнести большие сложности получения и приёма однополосного сигнала.
Ещё одним видом линейной модуляции является квадратурная амплитудная модуляция (КАМ),


















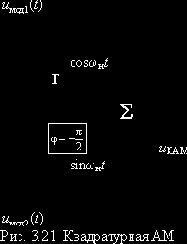
Контрольные вопросы
1. В чём существо амплитудной модуляции? Напишите аналитическое выражение АМ сигнала.
2. Что называют коэффициентом модуляции m? Как его можно определить по осциллограмме и спектрограмме АМ сигнала?
3. Нарисуйте спектр простого АМ сигнала.
4. Каков спектр сложного АМ сигнала?
5. От чего зависит ширина спектра АМ сигнала?
6. Укажите причины низкой энергетической эффективности амплитудной модуляции.
7. Нарисуйте векторную диаграмму простого АМ сигнала.
8. Нарисуйте схему параметрического амплитудного модулятора.
Укажите назначение её элементов.
9. Нарисуйте схему нелинейного амплитудного модулятора. Укажите назначение её элементов.
10. Что такое СМХ?
11. Как по СМХ определяют оптимальный режим работы амплитудного модулятора?
12. Назовите известные Вам виды линейной модуляции.
13. Нарисуйте спектр БМ сигнала.
14. Какую огибающую имеет БМ сигнал?
15. В чём суть однополосной модуляции? Каков спектр ОМ сигнала?
16. Приведите алгоритм и схему получения ОМ сигнала.
17. Нарисуйте схему получения сигнала КАМ.
Рекомендации по проведению экспериментальных исследований получения АМ, БМ, ОМ и КАМ сигналов
Для закрепления полученных в разделе 3.3 и 3.4 знаний полезно выполнить лабораторные работы № 8 «Амплитудная модуляция» в полном объёме (рис. 3.22) и № 11 «Линейные виды модуляции и синхронное детектирование» (рис. 3.23) в части, относящейся к исследованию модуляции, а также провести дополнительные экспериментальные исследования, используя иные виды сигналов в рамках предоставляемых этими работами ресурсов. Обратите, прежде всего, внимание на роль каждого ФУ в нелинейном и параметрическом амплитудных модуляторах, осциллограммы и спектрограммы сигналов в отдельных их точках. Укажите смысл СМХ, способ её экспериментального снятия и использования для определения оптимального режима модулятора. Для параметрических модуляторов укажите различия в них применительно к получению АМ, БМ, ОМ и
 |
Рис. 3.22. Исследование преобразований сигналов в параметрических ФУ |
 |
Рис. 3.23. Исследование преобразований сигналов в параметрических ФУ |
с линейными видами модуляции
При приёме модулированных сигналов над ними необходимо выполнять операцию обратную модуляции, т.е. преобразование, в результате которого будет получен сигнал, пропорциональный модулирующему на передающей стороне Такое преобразование называют детектированием, а выполняющий его ФУ – детектором.
Из сопоставления спектров модулирующего и модулированного сигналов (см., например, рис. 3.12) с очевидностью вытекает невозможность построения детекторов модулированных колебаний в классе линейных цепей.
Детектирование АМ сигналов


























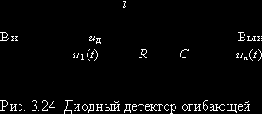


Проанализируем работу диодного детектора огибающей в режиме сильного сигнала. В этом случае целесообразно воспользоваться кусочно-линейной аппроксимацией вольтамперной характеристики (ВАХ)

- для вычисления uн(t) при известной нагрузке (R и C) надо предварительно определить ток i,
- для вычисления тока i при выбранном диоде (известной ВАХ ) надо знать напряжение на нём uд,

- для определения напряжения , надо знать искомое напряжение uн(t)











































Спектры сигналов в диодном детекторе ">


1)

2)

3)


4) сравнивают разность

При циклическом повторении этой процедуры с ростом числа приближений возможны два варианта:
- процесс последовательных приближений сходится к истинному решению,
- процесс расходится.
Для «удачного» выбора «нулевого» приближения и существенного сокращения числа итераций рекомендуется использование квазилинейного метода, в основе которого лежит допущение о форме искомого колебаний (вида функции), которым задаются с точность до его параметров.
Так, в нашем случае анализа диодного детектора, в качестве «нулевого» приближения к искомому напряжению на нагрузке примем постоянное напряжение





где S – крутизна наклонного участка ВАХ диода;

Уравнивая

Из (3.6) вытекает следующий результат

на основе которого можно сделать следующие выводы:
1. Угол отсечки q и, соответственно, Кдет не зависят от огибающей А, следовательно, детектирование в режиме сильного сигнала осуществляется линейно.
2. Для повышения эффективности детектирования (увеличения Кдет) следует стремиться к уменьшению угла отсечки q, что достигается увеличением произведения S×R.


















Диаграмма работы детектора огибающей wнt ">
4. Величину ёмкости С нагрузки следует определять из очевидного неравенства

Проведём анализ детектора огибающей в режиме слабого сигнала.
В этом случае ВАХ диода целесообразно аппроксимировать полиномом второй степени

Ограничимся определением «первого» приближения





В результате имеем (с учетом очевидного


При простом АМ сигнале, когда



Из полученного результата видно, что детектирование сопровождается нелинейными искажениями с коэффициентом гармоник

и можно сделать следующие выводы:
1. В режиме слабого сигнала имеет место квадратичное детектирование, сопровождаемое нелинейными искажениями.
2. Величина нелинейных искажений, определяемая


Детектирование БМ, ОМ и КАМ сигналов











1. Детектирование АМ сигналов
В этом случае

На выходе перемножителя получим


а на выход СД через ФНЧ пройдёт лишь первое (НЧ) слагаемое этого произведения

Для достижения наибольшего коэффициента детектирования


2. Детектирование двухполосных (БМ) сигналов
В этом случае (3.5)

На выходе перемножителя имеем


После ФНЧ на выходе СД получим

где

3. Детектирование однополосных (ОМ) сигналов
В этом случае (3.6)

На выходе перемножителя получаем



После ФНЧ на выходе СД при условии


где

4. Детектирование и разделение КАМ сигналов
В этом случае (см. рис 3.21)

На выходе перемножителя получаем



После ФНЧ на выходе СД имеем:
при условии


при условии



























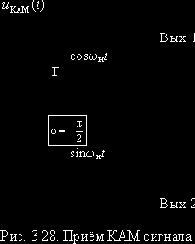


Выводы
1. Синхронный детектор позволяет детектировать сигналы с любым видом линейной модуляции без искажений независимо от уровня сигнала.
2. Синхронный детектор обладает наряду с амплитудной ещё и фазовой чувствительностью, что позволяет использовать его в качестве измерителя разности фаз входного и опорного колебаний (фазового детектора).
3. Отсутствие в СД синфазности несущего и опорного колебаний

- при приёме АМ и БМ сигналов – к уменьшению коэффициента детектирования ;

- при приёме ОМ сигналов – к искажению формы выходного сигнала за счёт суммирования , что, впрочем, не является существенным при приёме звуковых сообщений, т.к. эти искажения связаны с изменение фазового спектра сигнала при сохранении амплитудного (см. свойства преобразования Гильберта), а слуховой аппарат человека не обладает чувствительностью к фазовым искажениям;

- при приёме КАМ сигналов – к перекрёстным искажениям (не полному разделению сигналов), когда


Контрольные вопросы
1. Нарисуйте схему детектора огибающей. Приведите спектры сигналов в её отдельных точках.
2. Каковы особенности работы детектора огибающей в режиме сильного сигнала?
3. Каковы особенности работы детектора огибающей в режиме слабого сигнала?
4. Как выполняют детектирование БМ, ОМ и КАМ сигналов?
5. Нарисуйте схему синхронного детектора и спектры сигналов в отдельных её точках.
6. Как влияет на качество детектирования АМ, БМ и ОМ сигналов неточность восстановления фазы опорного колебания?
7. Как влияет на качество разделения сигналов с КАМ неточность восстановления фазы опорного колебания?
Рекомендации по проведению экспериментальных исследований детектирования АМ, БМ, ОМ и КАМ сигналов
Для закрепления полученных в разделе 3.5 знаний целесообразно выполнить лабораторные работы № 9 «Детектирование АМ сигналов» (рис. 3.29), № 21 «Детектор огибающей сигнала» (рис. 3.30) в полных объёмах и № 11 «Линейные виды модуляции и синхронное детектирование» (рис. 3.31) в части исследования синхронных детекторов. Обратите внимание на роль каждого ФУ в нелинейном и параметрическом детекторах, осциллограммы и спектрограммы сигналов в отдельных их точках, на причины и характер искажений сигналов при использовании нелинейных и параметрических детекторов.
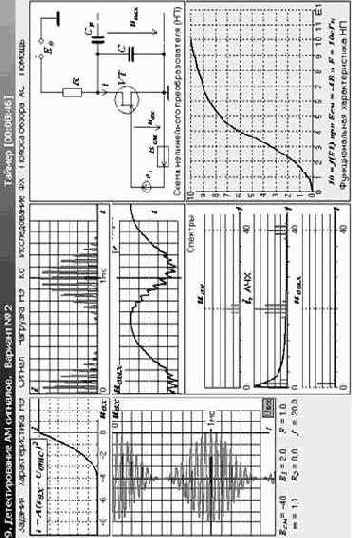 |
Рис. 3.29. Исследование транзисторного детектора АМ сигнала |
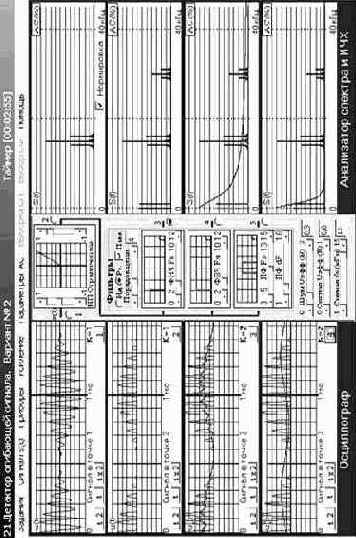 |
Рис. 3.30. Исследование детектора огибающей АМ сигнала |
 |
Рис. 3.31. Исследование синхронного детектиролвания АМ, БМ ОМ и КАМ сигналов |
3.6. Преобразование частоты сигналов
Преобразованием частоты называют перенос (транспонирование) спектра сигнала (обычно узкополосного) по оси частот «вверх» или «вниз» на некоторое расстояние wг, задаваемое гетеродином – маломощным генератором гармонического колебания

Преобразователь частоты состоит из смесителя частот и гетеродина (рис. 3.32 ).


Схема, приведённая на рис.3.20, может быть использована в качестве параметрического преобразователя частоты без каких либо изменений. Нелинейный преобразователь частоты может быть выполнен также по выше рассмотренной схеме амплитудного модулятора (рис. 3.16) при настройке нагрузочного колебательного LC контура на промежуточную частоту

 |
Рис. 3.33. Исследование параметрического преобразователя частоты |

Контрольные вопросы
1. Какой ФУ называют преобразователем частоты?
2. Приведите алгоритм и схему параметрического преобразователя частоты.
3. Объясните назначение каждого элемента схемы параметрического преобразователя частоты .
4. Нарисуйте схему преобразователя частоты на нелинейной основе и объясните назначение её элементов.
5. Какие преимущества даёт использование преобразователя частоты в радиоприёмных устройствах?
Рекомендации по проведению экспериментальных исследований преобразования частоты сигналв
Для закрепления полученных в разделе 3.6 знаний полезно выполнить лабораторные работы № 12 «Преобразование частоты на параметрической основе» (рис. 3.33) и №10 «Преобразование частоты сигналов на нелинейной основе» в полных объёмах. Обратите внимание на роль каждого ФУ в нелинейном и параметрическом преобразователях частоты, осциллограммы и спектрограммы сигналов в отдельных их точках.
3.7. Угловая (ЧМ и ФМ) модуляция
При угловой модуляции (УМ) информация о модулирующем сигнале закладывается в полную фазу


В зависимости от того, как это делается, различают два варианта УМ:
1) фазовая модуляция (ФМ), при которой

2) частотная модуляция (ЧМ), при которой

Поскольку фаза



то столь же тесно связаны между собой ФМ и ЧМ.
В частности, при ФМ

а при ЧМ

Из этих соотношений вытекает возможность получения обоих видов угловой модуляции с помощью одного типа модулятора (либо фазового, либо частотного) (рис. 3.34).
Векторная диаграмма колебания с УМ Из аналитического выражения колебания с УМ (3.8) видно, что его амплитуда U0 сохраняется неизменной, следовательно, вектор комплексной амплитуды

плоскости (рис. 3.35). Годограф этого вектора представляет
собой окружность.
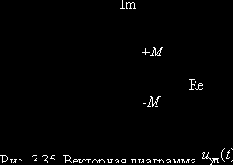
































где М – максимальное отклонение фазы от среднего значения называют индексом модуляции.
Изменение мгновенной частоты простого колебания с УМ происходит по закону

где




Из теории функций Бесселя известно, что

где Jk(M) – функции Бесселя первого рода порядка k от аргумента М (k = 0, ±1, ±2,…). Они обладают свойством

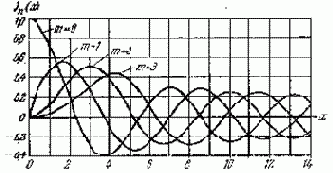
Рис. 3.36. Графики функций Бесселя
Подставляя (3.10) в (3.9), получаем

Вернёмся к действительному сигналу

Спектр простого сигнала с УМ, соответствующий полученному выражению, приведён на рис. 3.37.
Для определения ширины спектра простого сигнала с
















Таким образом, при М >> 1

и можно считать, что ширина спектра простого колебания с УМ вдвое больше его девиации частоты и существенно больше (в М раз) ширины спектра АМ сигнала.
При М << 1 достаточно в спектре этого колебания удержать первую пару боковых и считать его ширину

равной ширине спектра простого АМ сигнала.
Методы осуществления угловой модуляции
Различают два основных метода осуществления угловой модуляции – прямой и косвенный. По прямому методу реализуют частотные модуляторы на основе генераторов, частота колебаний которых управляется внешним напряжением (ГУН) (рис. 3.38). Особенностью ГУН является включение в его колебательную систему, от собственной частоты w0 которой зависит частота wг генерируемых колебаний, уп-равляемого реактивного элемента (УРЭ). В качестве УРЭ можно использовать варикап, «реактивный транзистор», ёмкость (индуктивность) которых зависит от приложенного напряжения (протекающего тока).
Достоинством прямого метода является возможность















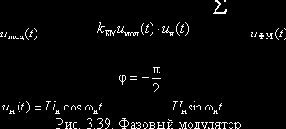 |
По косвенному методу реализуют фазовые модуляторы на основе схемы, представленной на рис. 3.39. Выясним условия, при которых эта схема обеспечивает ФМ. На выходе сумматора имеем



При выполнении условия


Таким образом установили, что рассмотренная схема может служить фазовым модулятором только при выполнении указанного неравенства, иначе говоря, только при малом индексе модуляции (М<<1) выходного сигнала uФМ(t). Это её основной недостаток, а достоинством является высокая стабильность несущей частоты uФМ(t) при использовании высокостабильного генератора несущего колебания.
3.8. Детектирование сигналов с угловой модуляцией
Детектирование ФМ сигналов Для детектирования ФМ сигналов можно использовать ранее рассмотренный синхронный детектор (рис. 3.27). При









Детектирование ЧМ сигналов Для построения частотных детекторов используются два метода связанные с преобразованием вида модуляции:
1) преобразование ЧМ в АМ с последующим амплитудным детектированием,
2) преобразование ЧМ в ФМ с последующим фазовым детектированием
Первый метод реализован в схеме частотного детектора с расстроенными контурами (рис. 3.41). Преобразователь ЧМ в АМ выполнен на двух колебательных контурах, расстроенных относительно частоты сигнала



























































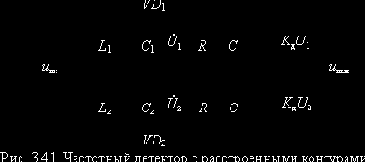



где Uс – амплитуда входного сигнала

m - коэффициент передачи входного трансформатора,

1-го контура,

2-го контура.


Выводы
1. Частотный детектор с расстроенными контурами работает по методу преобразования ЧМ в АМ с последующим амплитудным детектированием.
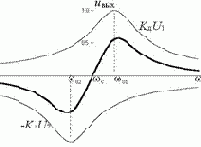
2. Достоинством данного частотного детектора является возможность достижения высокой крутизны его ХД.
3. Основной недостаток – сложность настройки. От неё зависит степень линейности рабочего участка ХД.
4. Частотный детектор (рис. 3.41) целесообразно использовать при приёме сигналов с цифровой ЧМ, когда важна крутизна ХД, а степень её линейности роли не играет.
































































где g - коэффициент пропорциональности,

Dj – фазовый сдвиг между




где М – взаимная индуктивность между L1 и L2,

r – сопротивление потерь контура,
Q – добротность контура,





где

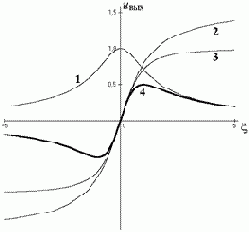
1)

2) arctgx,
3) sin(arctgx).
Рис. 3.44. Характеристика детектирования частотного дискриминатора
Выводы 1. Частотный дискриминатор реализует метод преобразования ЧМ в ФМ с последующим фазовым детектированием.
2. Частотный дискриминатор прост в настройке, т.к. его контур настраивается на частоту сигнала

3. Обеспечивается высокая степень линейности рабочего участка ХД вне зависимости от настройки контура.
4. Частотный дискриминатор целесообразно применять при приёме сигналов с аналоговой ЧМ, когда важна линейность ХД.
Контрольные вопросы
1. Дайте определения видам модуляции: угловая, фазовая, частотная.
2. Каким образом можно с помощью фазового модулятора получить ЧМ сигнал?
3. Каким образом можно с помощью частотного модулятора получить ФМ сигнал?
4. Что представляет собой векторная диаграмма колебания с угловой модуляцией?
5. Дайте определения индексу модуляции и девиации частоты. Какая между ними связь?
6. Какой спектр имеет простое колебание с УМ?
7. Как определяют практическую ширину спектра ФМ и ЧМ сигналов?
8. Нарисуйте схему фазового детектора. Какой вид имеет его ХД?
9. Какие методы используются при построении частотных детекторов?
10. Нарисуйте схему частотного детектора с расстроенными контурами.
11. Напишите аналитическое выражение ХД частотного детектора с расстроенными контурами, нарисуйте и объясните её форму.
12. Нарисуйте схему частотного дискриминатора.
13. Напишите аналитическое выражение и нарисуйте форму ХД частотного дискриминатора.
14. Проведите сравнительный анализ частотных детекторов разных типов.
Рекомендации по проведению экспериментальных исследований ФМ и ЧМ сигналов и фазового детектора
Для закрепления полученных в разделе 3.7 знаний полезно выполнить лабораторную работу № 4 «Модулированный сигналы» (из перечня тем виртуальной учебной лаборатории) в части исследования сигналов с фазовой и частотной модуляцией (рис. 3.45), а также провести дополнительные экспериментальные исследования, используя иные виды сигналов в рамках предоставляемых этими работами ресурсов.
Обратите внимание на общее и разное в ЧМ и ФМ сигналах при одном и том же модулирующем сигнале (особенно при использовании в качестве модулирующего сигнала гармонического колебания и импульсов треугольной формы). Убедитесь в расширении спектра ФМ и ЧМ сигналов с увеличением индекса модуляции, определите для каждого случая их практическую ширину.
Для закрепления полученных в разделе 3.8 знаний рекомендуется выполнить лабораторную работу № 13 «Детектирование ФМ сигналов» (рис. 3.46) в полном объёме, а также провести дополнительные экспериментальные исследования, используя иные виды сигналов в рамках предоставляемых этими работами ресурсов. Обратите внимание на вид экспериментально получаемой характеристики детектирования фазового детектора и на влияние выбора протяжённости её рабочего участка на степень искажений выходного сигнала.
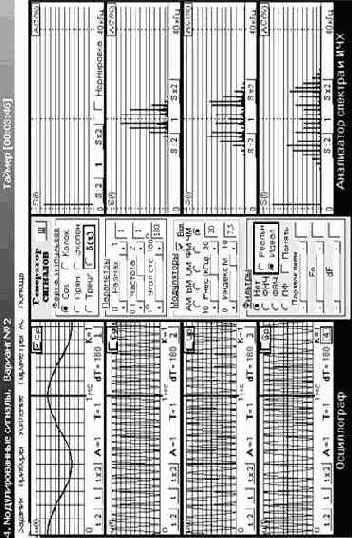 |
Рис. 3.45. Исследование сигналов с фазовой и частотной модуляциями |
 |
Рис. 3.46. Исследование фазового детектора |
3.9. Виды модуляции, используемые
при передаче дискретных сообщений
При передаче дискретных сообщений – последовательностей кодовых символов


где Т – длительность тактового интервала на котором передаётся один кодовый символ,
x(t) – функция, описывающая форму импульса на интервале Т.
Форму импульса x(t) выбирают из соображений ограничения его спектра полосой пропускания канала и удобства формирования (прямоугольную, гауссовскую, синусквадратичную). Для простоты дальнейших рассуждений ограничимся прямоугольной формой импульсов и использованием двоичного кода (m=2), алфавит которого содержит всего два символа b(0) = +1 и b(1) = –1. Тогда

При использовании гармонического переносчика модуляцию цифровым первичным сигналом называют цифровой (ЦМ). По виду модулируемого параметра различают цифровые амплитудную (ЦАМ), фазовую (ЦФМ) и частотную (ЦЧМ) модуляции.
Принципиальным отличием ЦМ от ранее рассмотренной аналоговой является конечный набор вариантов сигнала на выходе модулятора (в нашем случае всего два варианта s0(t) и s1(t) при передаче b0 и b1 соответственно). Это обстоятельство существенно меняют задачу приёма таких сигналов. При приёме сигналов с аналоговой модуляцией главным является воспроизведение формы модулирующего сигнала с минимальной погрешностью в результате его детектирования (непрерывного измерения информационного параметра). В случае приёма сигналов с ЦМ решается задача различения (обнаружения) вариантов сигналов с минимальной вероятностью ошибок (демодуляция). Вопросы демодуляции сигналов с цифровой модуляцией подробно будут рассмотрены во второй части курса ТЭС.
Описание сигналов с ЦМ во временной и спектральной областях можно рассматривать как частный случай аналогичного описания сигналов с аналоговой модуляцией, соответствующий конкретной форме модулирующего сигнала (3.14). В частности, имеем:
при ЦАМ


при ЦФМ



при ЦЧМ


где девиацию частоты Dw выбирают из условия обеспечения ортогональности сигналов s0(t) и s1(t).














Очевидно, что чем больше расстояние между сигналами, тем они надёжнее различаются при приёме на фоне помех. Следовательно, наибольшей помехоустойчивостью обладает ЦФМ, а наименьшей ЦАМ. На практике по причинам, которые будут понятны из материалов второй части курса ТЭС, вместо ФМ используют ОФМ (относительную фазовую модуляцию), отличающуюся тем, что модулирующий сигнал отображают не в абсолютной фазе гармонического переносчика, а в изменении его фазы по отношению к предыдущему сигналу.
Реализация модуляторов сигналов с ЦМ не вызывает сложностей и вытекает из аналитических выражений соответствующих сигналов (3.15) – (3.17).
Так, в частности, для получения сигнала с ЦАМ можно использовать параметрический амплитудный модулятор (рис. 3.15). В качестве фазового модулятора для получения сигнала с ЦФМ (3.16) можно использовать перемножитель, а сам сигнал рассматривать как БМ сигнал. Для получения сигнала с ЦЧМ можно использовать коммутатор двух генераторов с частотами


Общим недостатком рассмотренных простых видов ЦМ является низкая скорость передачи

Так, широко используется четырёхфазная ФМ-4 (ОФМ-4) (иное название – двукратная ФМ (ДФМ)), основанная на передаче четырёх сигналов, каждый из которых несёт информацию о двух битах (дибите) исходной двоичной последовательности. (00, 01, 10, 11). Соответственно фаза сигнала может принимать значения 0°, 90°, 180°, 270° (возможный вариант 45°, 135°, 225°, 315°). В результате при сохранении длительности сигнала Т на выходе модулятора достигается двукратное увеличение скорости передачи. Обычно такой сигнал формируют с помощью квадратурного модулятора (рис. 3.48). На его входы подают нечётные x(t) и чётные y(t) импульсы, получаемые из исходной двоичной последовательности с помощью регистра сдвига.
























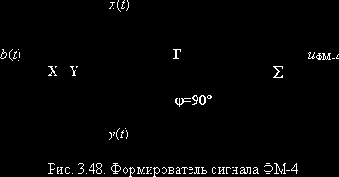
Графические интерпретации сигналов ФМ-4, ФМ-16 и КАМ-16 приведены на рис. 3.49. На комплексной плоскости сигналы отображены сигнальными точками (концами векторов их комплексных амплитуд), образующими сигнальное созвездие (signal constellation).




















































где L – число различных уровней системы сигналов КАМ,
М – число различных фаз системы сигналов ФМ.
Видно, что при увеличении значения М и одинаковой максимальной мощности сигналов системы КАМ предпочтительнее систем с ФМ. В частности, при М = 16 (L = 4)






Выводы
1. В системах передачи дискретных сообщений используются как простые виды цифровой модуляции ЦАМ, ЦЧМ, ЦФМ (ОФМ) при низких скоростях передачи, так и многопозиционные ФМ (ОФМ) и комбинированные КАМ при повышенных скоростях передачи.
2. Определяющим моментом при выборе системы ЦМ модуляции является число сигналов и минимальное расстояние между ними.
3. Чем больше сигналов используется в системе ЦМ, тем выше скорость передачи. Однако, выигрыш в скорости передачи сопровождается ухудшением различимости сигналов за счёт уменьшения расстояния между ними.
4. Многоуровневые системы КАМ предпочтительнее многофазных систем ФМ (ОФМ).
Контрольные вопросы
1. Перечислите известные Вам виды цифровой модуляции гармонического переносчика.
2. В чём принципиальное отличие цифровой модуляции и демодуляции от аналоговой?
3. Напишите аналитические выражения сигналов с ЦАМ, ЦФМ, ЦЧМ.
4. Что общего и различного в системах цифровой модуляции ФМ и ОФМ?
5. Изобразите сигналы с разными видами цифровой модуляции в виде векторов в пространстве сигналов и оцените их сравнительную различимость.
6. Какими способами повышают скорость передачи сигналов с цифровой модуляцией?
7. Нарисуйте схему формирования сигналов ФМ-4 и объясните принцип её работы.
8. Что представляют собой сигнальные созвездия?
9. Почему многопозиционные системы КАМ предпочтительнее систем ФМ (ОФМ).
Рекомендации по проведению экспериментальных исследований формирования сигналов с разными видами цифровой модуляции
Для закрепления полученных в разделе 3.9 знаний полезно выполнить лабораторные работы № 23 ÷ №28, связанные с исследованиями процессов формирования сигналов с разными видами цифровой модуляции:
- ФМ и ОФМ (рис. 3.50),
- ФМ-4 (QPSK) (рис. 3.51),
- ФМ-4 со сдвигом (OQPSK) (рис. 3.52),
- ФМ-16 (рис. 3.53),
- КАМ-4 (QASK) (рис. 3.54),
- КАМ-16 (SPM) (рис. 3.55).
Наблюдайте появление паразитной амплитудной модуляции при прохождении сигналов с разными видами ФМ через полосовой фильтр. Исследуйте влияние на пик-фактор сигналов с четырёхкратной ФМ от способа их формирования (ФМ и ФМ-4 со сдвигом).
Сравните расстояния между сигнальными точками сигнальных созвездий для сигналов с разными видами цифровой модуляции, особенно для сигналов с равными их количествами (ФМ-16, КАМ-4 (QASK) и КАМ-16 (SPM)). Обратите внимание на независимость этих расстояний от фазовых сдвигов сигналов в канале (фазовращателе).
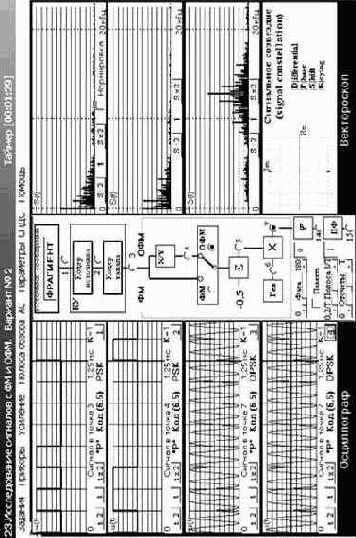 |
Рис. 3.50. Исследование сигналов с ФМ и ОФМ |
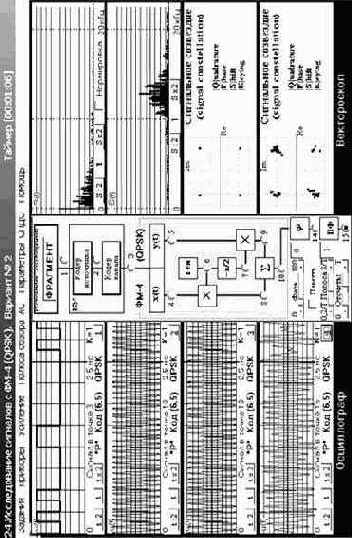 |
Рис. 3.51. Исследование сигналов с ФМ-4 (QPSK) |
 |
Рис. 3.46. Исследование сигналов с ФМ-4 со сдвигом (OQPSK) |
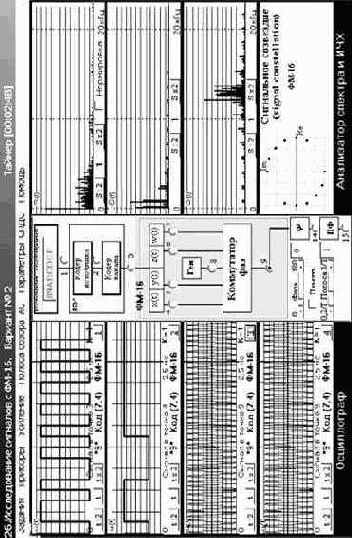 |
Рис. 3.46. Исследование сигналов с ФМ-16 |
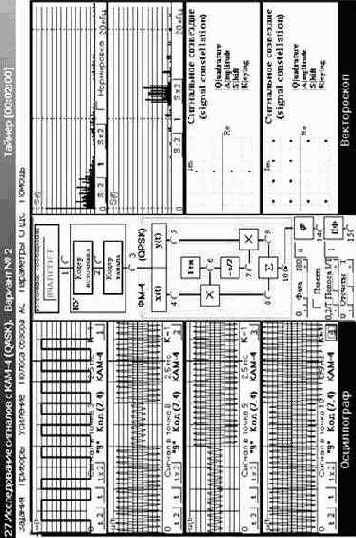 |
Рис. 3.46. Исследование сигналов с КАМ-4 (QASK) |
 |
Рис. 3.46. Исследование сигналов с КАМ-16 (SPM) |





